Четырехугольная пирамида в задаче C2
30.09.2018
Решая задачу C2 методом координат, многие ученики сталкиваются с одной и той же проблемой. Они не могут рассчитать координаты точек, входящих в формулу скалярного произведения. Наибольшие трудности вызывают пирамиды. И если точки основания считаются более-менее нормально, то вершины — настоящий ад.
Сегодня мы займемся правильной четырехугольной пирамидой. Есть еще треугольная пирамида (она же — тетраэдр). Это более сложная конструкция, поэтому ей будет посвящен отдельный урок.
Для начала вспомним определение:
Правильная пирамида — это такая пирамида, у которой:
В основании лежит правильный многоугольник: треугольник, квадрат и т.д.; Высота, проведенная к основанию, проходит через его центр.В частности, основанием четырехугольной пирамиды является квадрат. Прямо как у Хеопса, только чуть поменьше.
Ниже приведены расчеты для пирамиды, у которой все ребра равны 1. Если в вашей задаче это не так, выкладки не меняются — просто числа будут другими.
Вершины четырехугольной пирамиды
Итак, пусть дана правильная четырехугольная пирамида ,где — вершина, основание — квадрат. Все ребра равны 1. Требуется ввести систему координат и найти координаты всех точек. Имеем:
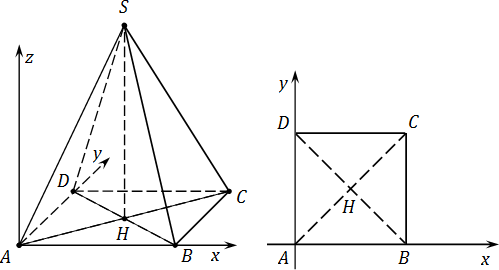
Вводим систему координат с началом в точке :
Ось направлена параллельно ребру ; Ось — параллельно . Поскольку — квадрат, ⊥ ; Наконец, ось направим вверх, перпендикулярно плоскости .Теперь считаем координаты. Дополнительное построение: — высота, проведенная к основанию. Для удобства вынесем основание пирамиды на отдельный рисунок. Поскольку точки , , и лежат в плоскости , их координата = 0. Имеем:
= (0; 0; 0) — совпадает с началом координат; = (1; 0; 0) — шаг на 1 по оси от начала координат; = (1; 1; 0) — шаг на 1 по оси и на 1 по оси ; = (0; 1; 0) — шаг только по оси . = (0,5; 0,5; 0) — центр квадрата, середина отрезка .Осталось найти координаты точки . Заметим, что координаты и точек и совпадают, поскольку они лежат на прямой, параллельной оси . Осталось найти координату для точки .
Рассмотрим треугольники и :
= = 1 по условию; Угол = = 90°, поскольку — высота, а ⊥ как диагонали квадрата; Сторона — общая.Следовательно, прямоугольные треугольники и равны по одному катету и гипотенузе. Значит, = = 0,5 · .Но — диагональ квадрата со стороной 1. Поэтому имеем:
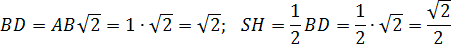
Итого координаты точки :
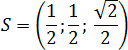
В заключение, выпишем координаты всех вершин правильной прямоугольной пирамиды:
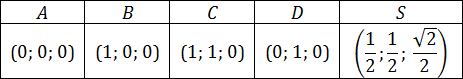
Что делать, когда ребра разные
А что, если боковые ребра пирамиды не равны ребрам основания? В этом случае рассмотрим треугольник :
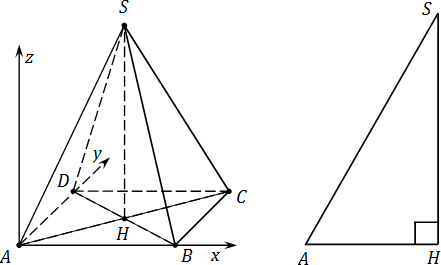
Треугольник —прямоугольный, причем гипотенуза — это одновременно и боковое ребро исходной пирамиды .Катет легко считается: = 0,5 · . Оставшийся катет найдем по теореме Пифагора. Это и будет координата для точки .
Задача. Дана правильная четырехугольная пирамида , в основании которой лежит квадрат со стороной 1. Боковое ребро = 3. Найдите координаты точки .
Координаты и этой точки мы уже знаем: = = 0,5. Это следует из двух фактов:
Проекция точки на плоскость — это точка ; Одновременно точка — центр квадрата , все стороны которого равны 1.Осталось найти координату точки . Рассмотрим треугольник . Он прямоугольный, причем гипотенуза = = 3,катет — половина диагонали. Для дальнейших вычислений нам потребуется его длина:
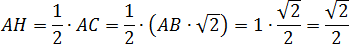
Теорема Пифагора для треугольника : 2 + 2 = 2. Имеем:
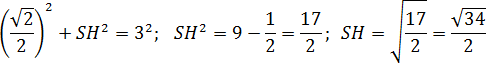
Итак, координаты точки :
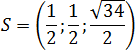
Смотрите также:
Четырехугольная пирамида: как найти координаты вершин Введение системы координат
Введение системы координат  Тест к уроку «Что такое логарифм» (средний)
Тест к уроку «Что такое логарифм» (средний)  Пробный ЕГЭ 2012. Вариант 10 (без логарифмов)
Пробный ЕГЭ 2012. Вариант 10 (без логарифмов)  Пробный ЕГЭ по математике 2015: 1 вариант
Пробный ЕГЭ по математике 2015: 1 вариант  Вебинар по задачам С1: тригонометрия
Вебинар по задачам С1: тригонометрия 





